Gravitometer Gambit

Last weekend, I played the HackTheBox University CTF with StudSec. More than 8,000 players signed up for this CTF.

This writeup explain how I solved the Gravitometer Gambit challenge during the CTF. Even though it was a hard reverse engineering challenge, I solved it only 4.5 hours after the start of the CTF, more than 24 hours earlier than the second team that solved it.

If you would like try the challenge yourself before reading the writeup, you can download the challenge here. Otherwise, feel free to read on.

Introduction
Initial Analysis
Initial Key Recovery
Full Key Recovery
Decrypting the Game Section
Analyzing the Game Section
Summary

Introduction

If we look at the challenge with file, we see that it is an ELF file that was compiled for 32-bit ARM CPUs:

$ file gravitometer
gravitometer: ELF 32-bit LSB executable, ARM, EABI5 version 1 (GNU/Linux), statically linked, BuildID[sha1]=3538250ae48ef27cf22c9dc9c0110f63f3ba27fa, for GNU/Linux 3.2.0, not stripped

Even though it is compiled for ARM, it can be executed normally on x86 if qemu-user is installed.

When we execute the program, we get the following prompt:

https://class.ece.iastate.edu/cpre288/resources/docs/Thumb-2SupplementReferenceManual.pdf
Dear traveller, you found an old manual floating around! In order to escape from the Rocky
Belt of Thumbs, you need to control the Gravitometer (me) and write the secret code. Make
sure you give me the correct serial number or you will have to restart! There are no function
calls to outside the code area (BL instruction). There is BLX (47 xx), with the args that
were passed in and propagate inside. Are you worthy of exploding me and setting me free?

Thumb-2 is an extension to the ARM instruction set that mixes 16-bit and 32-bit instructions. This might be relevant for the challenge. In any case, the program asks us to enter a serial number.

Initial Analysis

Luckily, I have purchased IDA Home for ARM, so I could easily decompile the program. In the binary, we see a .game section at 0x500000 that looks encrypted, and we find the main function in the .text segment. While there are many other functions as well, most of these are part of libc and not relevant for us.

In the main function, we see that the program reads a key from stdin and uses it to decrypt the .game section. It then performs some checks on the input key and decrypted .game section, and if the checks succeed, it calls a function in the decrypted .game section.

The decryption algorithm a kind of substitution cipher and works as follows:

def decrypt(data, key):
    for i in range(0x1000):
        if i % 2 or i >= 0x2DC:
            value = data[i]
            data[i] = key[value & 0xF] | (key[value >> 4] << 4)
        else:
            data[i] = key[data[i]]

For the first 0x2DC bytes, the bytes at even positions are substituted by bytes in the key. For the bytes at odd positions, and all bytes after the first 0x2DC, a weaker substitution method is used that only substitutes 4 bits at once. This will be important for our solution later on.

The checks that are performed next are somewhat arbitrary. While they leak some bytes of the key, we do not need them to solve the challenge:

strlen(&game[0x614]) == 0x39
input[0xAB] == 0x2D
game[0x269] == 0xE9
game[0x614] == 0x2D
input[7] == 7

After that, the program divides the .game section into blocks of 16 bytes, calculates their SHA-256 hash, and checks if each hash matches a specific value.

Initial Key Recovery

Our goal is to recover the key. It is important to realize that the key is a substitution box. Every value is simply mapped to another value. This means that, if we know what a value decrypts to at one position, we can decrypt all other occurrences of that value as well.

We can figure out values by brute forcing SHA-256 hashes. Brute forcing 16 unknown bytes at once would be impossible, but this is luckily not required. What saves is us is that the decryption algorithm is weak:

If a value appears multiple times in a block, we only need to brute force it once.
After we successfully brute force a value in one block, we no longer need to brute force it in any other block.
At many positions, only 4 bits are substituted at once, which reduces the number of values that we need to brute force.

Now, our basic algorithm to recover the key is as follows:

Find a block that can be brute forced in a reasonable amount of time, by determining the number of unknown values in each block.
After brute forcing the block, add the newly discovered values to the key. Every time a value is added to the key, more blocks should become brute forcable.
Repeat this process until the entire .game section can be decrypted.

We also make a few assumptions to improve the performance. Although the program does not enforce these, we can always make assumptions and roll back later if they turn out to be wrong:

Every byte value appears exactly once in the key.
The first 16 values in the key are all less than 16.

Now, we start by brute forcing the first 16 bytes of the key:

import hashlib

# None marks an unknown value
key = [None] * 16

with open("gravitometer", "rb") as f:
    data = f.read()

game = data[0x10000 : 0x11000]

hashes = []
for i in range(110):
    base = 0x58318 + 32 * i
    hashes.append(data[base : base + 32])

def crack_block(block, hash):
    global key

    # Split each byte into two halves of 4 bits each
    nybbles = []
    for byte in block:
        nybbles.append(byte & 0xF)
        nybbles.append(byte >> 4)

    # Find the values that are not yet known in the key
    unknowns = []
    for value in nybbles:
        if key[value] is None and value not in unknowns:
            unknowns.append(value)

    # Skip this block if it has too many unknowns or none at all
    if not 1 <= len(unknowns) <= 4:
        return

    # Try all combinations of values
    for i in range(16 ** len(unknowns)):
        updated_key = key.copy()
        for j in range(len(unknowns)):
            updated_key[unknowns[j]] = i % 16
            i //= 16

        # Decrypt the block with the current key
        decrypted = []
        for j in range(16):
            byte = block[j]
            byte = updated_key[byte & 0xF] | (updated_key[byte >> 4] << 4)
            decrypted.append(byte)

        # Check if the hash is correct
        if hashlib.sha256(bytes(decrypted)).digest() == hash:
            key = updated_key
            return

# Loop until all bytes of the key are known
while any(value is None for value in key):
    # Skip to the part where always 4 bits are substituted at once
    for i in range(0x2E0, 0x6E0, 16):
        block = game[i : i + 16]
        hash = hashes[i // 16]
        crack_block(block, hash)

print(key)

This script prints the first 16 bytes of the key in less than a second:

[11, 15, 9, 12, 10, 13, 0, 7, 2, 3, 5, 14, 4, 1, 8, 6]

Full Key Recovery

After recovering the first 16 bytes of the key, we can already decrypt half of the bytes in each block (the bytes at odd positions). This makes it much easier to brute force the remaining blocks. Again, we repeatedly pick a block that can be brute forced in a reasonable amount of time and add values to the key as we go:

import hashlib

key = [11, 15, 9, 12, 10, 13, 0, 7, 2, 3, 5, 14, 4, 1, 8, 6]
key += [None] * 240 # None marks an unknown value

# We assume that every value appears in the key exactly once.
# By keeping track of the remaining values we reduce the time
# that it takes to brute force.
options = list(range(16, 256))

with open("gravitometer", "rb") as f:
    data = f.read()

game = data[0x10000 : 0x11000]

hashes = []
for i in range(110):
    base = 0x58318 + 32 * i
    hashes.append(data[base : base + 32])

def crack_block(offset, block, hash, limit):
    global key

    # Find the values that are not yet known in the key
    unknowns = []
    for i in range(16):
        # We are only interested in byte at even positions below 0x2DC
        if i % 2 == 0 and offset + i < 0x2DC:
            value = block[i]
            if key[value] is None and value not in unknowns:
                unknowns.append(value)

    # Skip this block if it already solved
    if len(unknowns) == 0:
        return True

    # Count the number of values that we need to brute force
    # Skip this block if it has too many unknowns
    count = len(options) ** len(unknowns)
    if count > limit:
        return False

    print(f"Brute forcing {count} values")

    # Try all combinations of values
    for i in range(count):
        updated_key = key.copy()
        for j in range(len(unknowns)):
            updated_key[unknowns[j]] = options[i % len(options)]
            i //= len(options)

        # Decrypt the block with the current key
        decrypted = []
        for j in range(16):
            byte = block[j]
            if j % 2 == 0 and offset + j < 0x2DC:
                byte = updated_key[byte]
            else:
                byte = updated_key[byte & 0xF] | (updated_key[byte >> 4] << 4)
            decrypted.append(byte)

        # Check if the hash is correct
        if hashlib.sha256(bytes(decrypted)).digest() == hash:
            # Update the key and remove the new values from the options
            key = updated_key
            for value in key:
                if value in options:
                    options.remove(value)

            print(f"Recovered {256 - key.count(None)} bytes of the key")
            return True

    raise ValueError("Failed to brute force block")

limit = 2 ** 16
while True:
    cracked = []
    for i in range(0, 0x2E0, 16):
        block = game[i : i + 16]
        hash = hashes[i // 16]
        result = crack_block(i, block, hash, limit)
        cracked.append(result)

    print(f"Cracked {cracked.count(True)} / 46 blocks")

    # Check if we are done
    if all(cracked):
        break

    # Increase the limit a bit
    limit *= 2

print(key)

Without optimizing the script further, it takes about 20 minutes to complete, with the last few bytes of the key taking most of the time. While many bytes of the key are still unknown, that is not a problem because these are unused during decryption.

Decrypting the Game Section

Since we have recovered the key, we can now decrypt the .game section in the program:

key = [
    11, 15, 9, 12, 10, 13, 0, 7, 2, 3, 5, 14, 4, 1, 8, 6,
    None, None, None, None, None, None, 76, 96, 65, 67, 33, None, None, None, 221, None,
    25, None, None, None, None, 179, None, None, 103, None, None, None, None, None, None, None,
    51, None, 132, None, None, None, None, None, None, 74, None, None, 233, None, None, None,
    169, 245, None, None, None, None, None, None, 84, None, 193, None, None, 90, 237, None,
    155, None, 162, None, 72, 32, None, None, None, None, None, None, None, None, None, 56,
    64, 52, None, 23, None, None, None, None, 129, None, 192, 236, None, None, 102, 131,
    146, 227, None, None, None, None, 167, None, 145, None, 22, None, 244, None, 220, 164,
    57, 248, None, 120, 180, None, 251, 243, None, None, None, None, 89, 112, None, None,
    None, None, 24, None, None, 36, None, None, None, None, None, None, None, 217, None, 138,
    18, None, None, 188, 20, None, 87, None, 61, None, 55, 45, 255, 218, 216, 91,
    228, None, None, None, 157, None, None, 161, None, None, 202, 189, None, None, None, None,
    None, 19, None, 148, None, 79, None, 176, 98, None, 172, 195, None, None, 128, 17,
    None, None, None, 97, None, 160, 232, None, 130, 250, 88, None, 223, 240, 26, None,
    None, 241, 249, None, 238, 73, 99, None, 16, 80, None, None, 231, None, 147, 242,
    168, 48, None, 104, None, None, 225, None, None, None, None, None, None, 85, None, None
]

with open("gravitometer", "rb") as f:
    data = f.read()

game = bytearray(data[0x10000 : 0x11000])
for i in range(0x1000):
    if i % 2 or i >= 0x2DC:
        value = game[i]
        game[i] = key[value & 0xF] | (key[value >> 4] << 4)
    else:
        game[i] = key[game[i]]

data = data[:0x10000] + game + data[0x11000:]

with open("gravitometer_patched", "wb") as f:
    f.write(data)

This script generates a new binary but with a decrypted .game section. We can now load it into IDA again.

Analyzing the Game Section

The game starts at address 0x500268. This function is called with the following function pointers as arguments: srand, rand, printf, scanf, malloc, free and exit. After looking at the code for a while, I got a rough idea of what it does.

We should enter 168 bytes encoded in hex.
Our input is transformed in some way and inserted into an irregular 16x16 sudoku.
If the sudoku is valid, the flag is printed, which simply contains the values that are entered into the sudoku in uppercase.

The shape of the sudoku is defined at 0x5002E4:

The prefilled values are defined at 0x5003E4, right after the shape:

A 255 means that the cell is empty and will be filled from the user input. It would be time consuming to solve the whole sudoku by hand, but luckily online solvers exist. After entering the shape and values into the solver, we quickly get the solution:

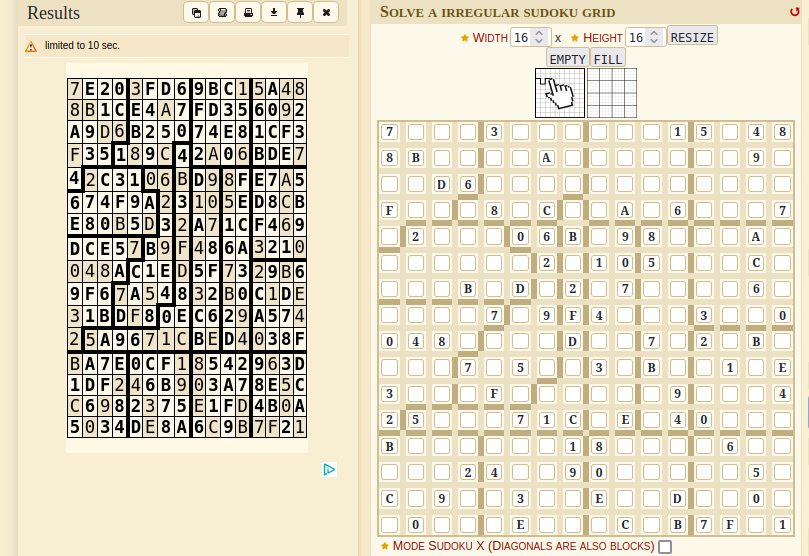
Now, there is only one more thing that we need to solve. Rather than filling the sudoku from top to bottom, the program fills each shape of the sudoku separately, in an arbitrary order. The order depends on the random numbers that are generated with a fixed seed. Because the program uses the standard RNG from libc, we can easily simulate that with Python.

By taking the sudoku shape from the program, the solution that was generated by the solver, and the order that we generate with rand(), we can finally obtain the flag:

import ctypes

libc = ctypes.CDLL("libc.so.6")
libc.srand(1337) # This is the seed

# Generate the order in which the shapes are filled
order = []
while len(order) < 16:
    value = (libc.rand() & 0xF) + 1
    if value not in order:
        order.append(value)

# The solution that was produced by the online solver
solution = """
7E203FD69BC15A48
8B1CE4A7FD356092
A9D6B25074E81CF3
F35189C42A06BDE7
42C3106BD98FE7A5
674F9A23105ED8CB
E80B5D32A71CF469
DCE57B9F486A3210
048AC1ED5F7329B6
9F67A54832B0C1DE
31BDF80EC629A574
25A9671CBED4038F
BA7E0CF18542963D
1DF246B903A78E5C
C6982375E1FD4B0A
5034DE8A6C9B7F21
"""

solution = solution.replace("\n", "")

# Read the sudoku shapes and prefilled values from the program
with open("gravitometer_patched", "rb") as f:
    data = f.read()

shape = data[0x102E4 : 0x103E4]
values = data[0x103E4 : 0x104E4]

flag = ""
for shape_id in order:
    for index in range(256):
        if shape[index] != shape_id: continue
        if values[index] != 255: continue
        flag += solution[index]

print("HTB{" + flag + "}")

This prints the following flag: HTB{A7E1DF6853496CDA5738F93D8EC4BA2C31674F9AE805DA85F2C6B0CF6B275D8A4380EA963BC1EA4D8DCE5A9F61BFE1C6A302D5423A71F69A6021CF3BDEE75D8BF4921E201CA93549BCFD3574E820FD6E47B25019}

Summary

The challenges consisted of two stages. The first stage involved brute forcing SHA-256 hashes in a smart way. The second stage involved solving a sudoku and simulating an RNG-based algorithm. The most difficult parts of this challenge were figuring out a good way to brute force the hashes in the first stage, and figuring out the logic in the second stage. Since the challenge required a good understanding of the logic in the program, and the solution could be scripted quite well, it was a fun challenge to solve.